Keplerovy zákony pohybu planet
Ještě předtím, než Newton formuloval zákon všeobecné gravitace, si Johannes Kepler všiml, že pohyb planet se řídí třemi jednoduchými zákony, které se s velkou přesností shodují s výsledky měření poloh planet.
Keplerovy zákony zdokonalily heliocentrickou teorii Mikuláše Koperníka tím, že nahradily kruhové dráhy eliptickými a popsaly změny rychlosti pohybu planet.
Znění Keplerových zákonů
První Keplerův zákon: Každá planeta obíhá po eliptické dráze, přičemž Slunce se nachází v jednom z ohnisek této elipsy.
Druhý Keplerův zákon (zákon stejných polí): Čára spojující Slunce a planetu obíhá stejná pole ve stejných intervalech.
Keplerův třetí zákon: Krychle velkých poloos oběžných drah libovolných dvou planet se k sobě vztahují jako čtverce jejich dob oběhu (velká poloosa je polovinou nejdelšího pásu elipsy). Třetí Keplerův zákon je jedinou klasickou přímou metodou pro určení hmotnosti kosmických těles. Určení relativní hmotnosti Jupiteru vzhledem ke Slunci na základě údajů o oběhu měsíce Callisto provedl již Newton v Principiích.
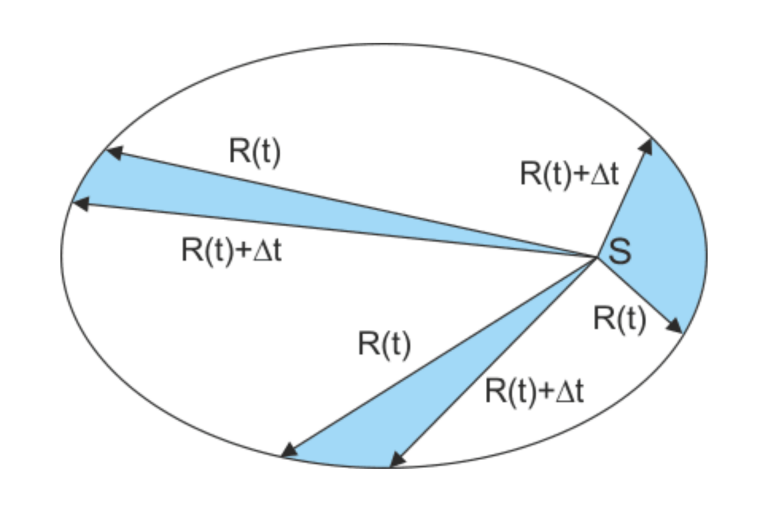
Z druhého Keplerova zákona vyplývá, že planety (nebo přirozené družice) by se měly pohybovat rychle v blízkosti Slunce (když je vektor R(t) nejkratší) a stále pomaleji, jak se od Slunce vzdalují (když vektor R(t) roste). Dobrým příkladem je Halleyova kometa, která oběhne kolem Slunce za 76 let, z nichž pouze jeden rok stráví v blízkosti Slunce (pak je ze Země neviditelná).

Z třetího Keplerova zákona vyplývá, že čím větší je oběžná dráha planety, tím větší je perioda jejího oběhu kolem Slunce.
| Planeta | Vzdálenost od Slunce (AU) | Doba oběhu (dnů) |
|---|---|---|
| Merkur | 0,39 | 87,97 |
| Venuše | 0,72 | 224,70 |
| Země | 1,00 | 365,26 |
| Mars | 1,52 | 686,98 |
| Jupiter | 5,20 | 4332,82 |
| Saturn | 9,54 | 10775,60 |
| Uran | 19,19 | 30687,15 |
| Neptun | 30,06 | 60190,03 |
Newton ukázal, že Keplerovy zákony lze odvodit z principů dynamiky. Například ukázal, že pouze pokud je síla nepřímo úměrná čtverci vzdálenosti, pak jsou splněny první a třetí Keplerův zákon.